Introduction to Tree Selection Sorting

Question

Maybe you like me have a question: Why heap sorting using a binary tree, but it is called heap sorting, rather than tree sorting?

Because the predecessor of heap sort is called Tree Selection Sorting, it also uses a tree structure, but is slightly simpler. Finally we will talk about why invent heap sorting to replace tree sorting.

Donald E. Knuth described the tree selection sorting algorithm like a table tennis game, so here we use an example from TAOCP. Suppose there are eight people participating in the competition and they need to judge the winner to eighth place. The schedule is as follows:

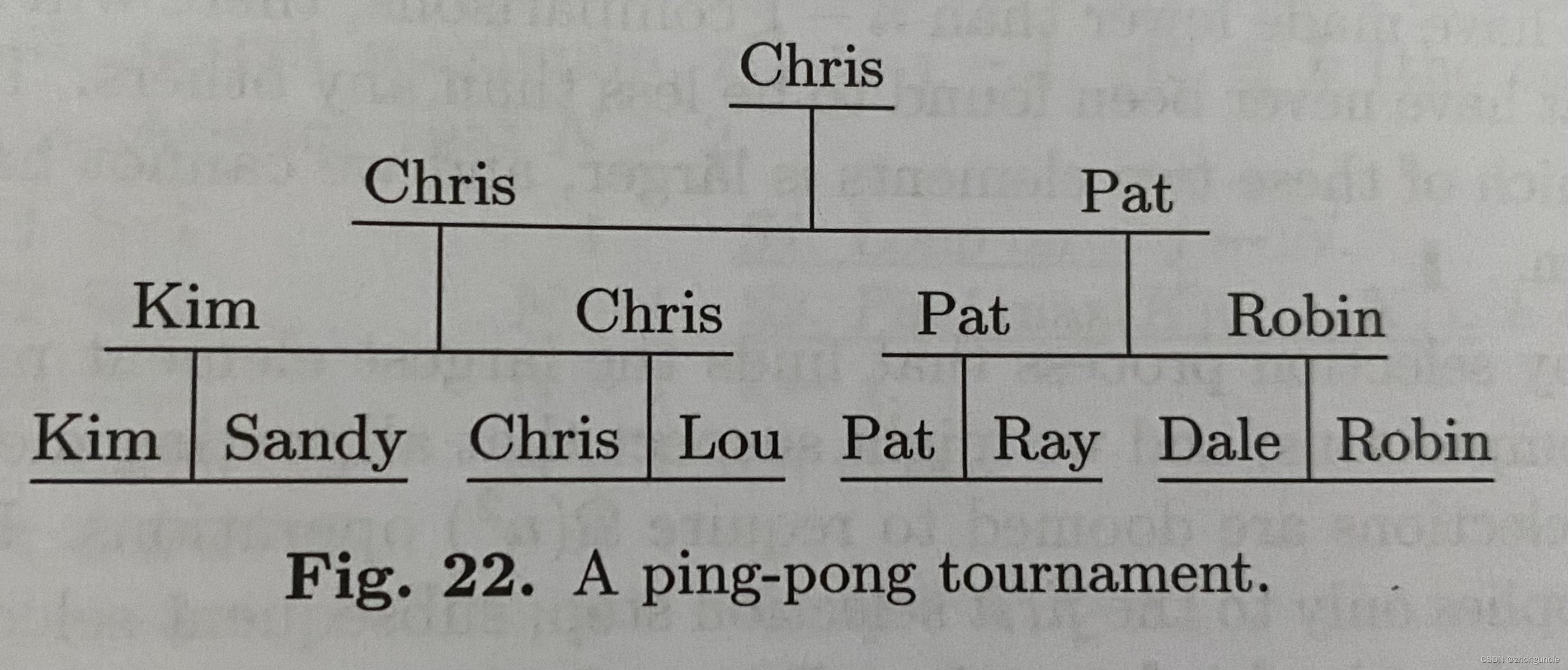
Kim and Sandy, Chris and Lou, Pat and Ray, Dale and Robin compete in groups and the winner advances. There is a winner after 7 games, the final champion was Chris, but who was second? Is it Pat? Not must be Pat, because although Kim and Lou both lost to champion Chris, they are not necessarily lose to Pat, so Kim and Lou still need to have a game, and then the winner will have a game with Pat (You may be wondering why Sandy doesn’t have to compete with Pat. It’s because Sandy is already weaker than Kim. No matter what the situation is, Sandy never be second). By analogy, the sorting can finally be completed.

In this schedule tree, the root is the champion. And after each winner is selected, the remaining people will be rematched (Mr. Knuth design even if the athletes are sick or in bad condition, they will have to rematch. You may think it is unfair, but we don’t consider it here).

Algorithm

There are two versions of tree selection sort, the original version and an improved version proposed by K. E. Iverson in 1962.

Original version

The specific steps of the original version tree sorting are as follows:

1. In the first step, compare all nodes pairwise, select the minimum value 1, and output it (In TAOCP, delete this element from the original array);
2. Then compare the remaining elements and output min one by one until the end. As shown below.

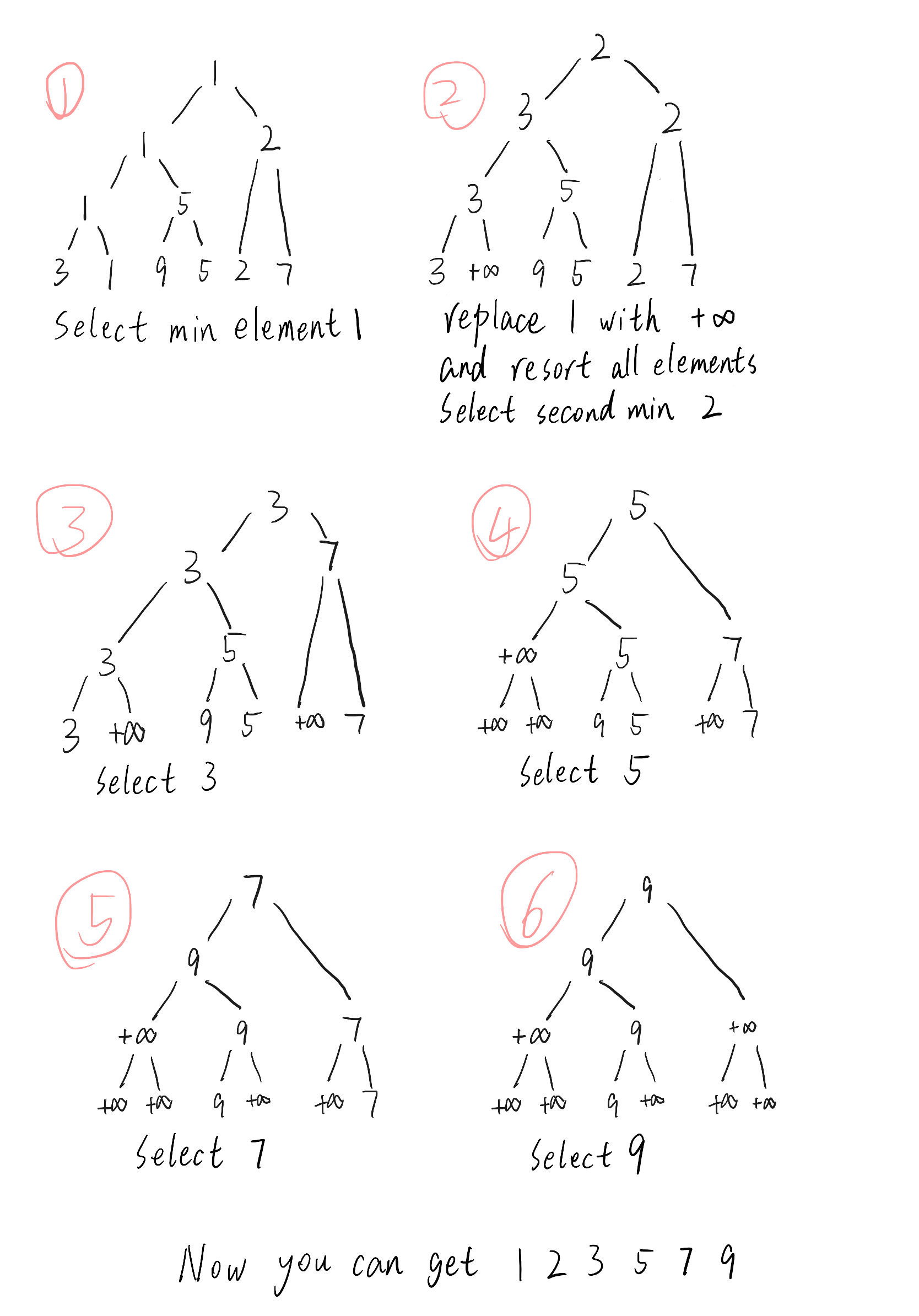
In this algorithm, replace the position of the original minimum value with +∞ every time after outputting the selected minimum value, so need to know the pointer or subscript of each element. (I guess you are curious about how represent +∞ in the code, so I will talk them at the end)

Therefore, the space required is divided into three parts: N keywords, N-1 pointers and N locations or pointers to store the output. However, if in array, it is just two arrays.

Because each re-comparison only change one path (you can see from image above), so selecting the second minimum value only takes lg N times at most (N is the number of elements), so comparing all elements requires NlgN.

Improved version

An improved version of tree sorting uses the “Pater Principle”. Personally, I feel that Mr. Knuth’s use of the word “Pater Principle” is not very precise, but the meaning is very appropriate, and can’t find a better word (but they don’t have any relationship because improvements to tree sorting were in 1962, and the “Pater Principle” developed in 1968).

The Peter Principle is a management concept developed by Laurence J. Peter. You can see it in https://en.wikipedia.org/wiki/Peter_principle.

For short, in a system, if a person is successfully promoted, he will eventually reach a position that exceeds his ability, and then he will not be able to continue to be promoted. But the company will not fire him, he stay in this position (it is a very interesting principle).

The improved version is to compare the values of leaf nodes and place them in the appropriate position, then delete the previous nodes, which can greatly reduce the number of comparisons. Like this:

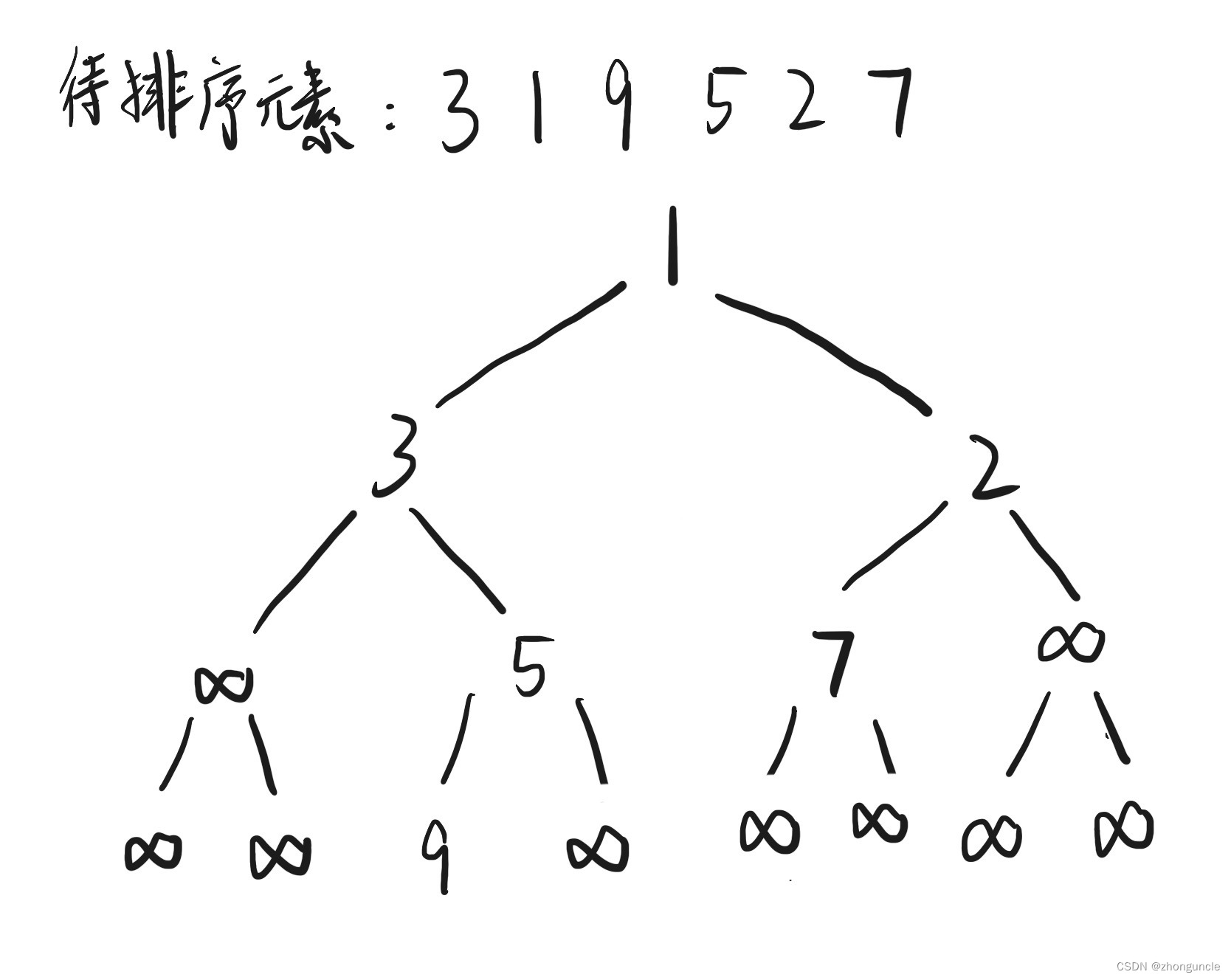
If ignore +∞, the order of elements should be 1 3 2 5 7 9. If you run the improved version iteratively, you will find that after some iterations, the final binary tree will “jump repeatedly” between the two situations. So we need to improve it, and this method is heap sort. That is why invent heap sort.

Or after the first tree selection sort, you can use direct selection sort algorithm. Because now the elements are much more ordered than before, it will be faster to use an unstable sorting method now. For example, only the positions of 3 and 2 are wrong at this time, and it will be much faster to select directly.

I hope these will help someone in need~