What is complement graphs, isomorphic graphs, and self-complement graphs?

Many articles on the Internet do not explain the complement graph, isomorphic graph, and self-complement graph in a very clear way, so I will write a short note to record it.

Isomorphic graph

The mathematical definition of an isomorphic graph is: given two graphs G=(V,E) and G'=(V',E'), if there exists a bijective function f:V->V' such that for any vertex u,v∈V, (u,v)∈E if and only if (f(u),f(v))∈E', then G and G' are isomorphic graphs.

The mathematical definition looks complicated, but in short, the two graphs have the same points and edges, but the positions of the points are different. Here is an explanation of what “the same points and edges are the same”: the degree of a point does not change, and the points at both ends of an edge do not change. These point numbers, edge numbers, and degree sequences are also called graph properties. Isomorphic graphs are graphs that have the same properties.

Take a look at the following very common isomorphic graph. You can see that both graphs have 5 points and 5 edges. The degree of each point is 2. Only the position has changed, and the properties of the graph have not changed. So another explanation for isomorphic graphs is that if you can move the points, the graph is isomorphic.

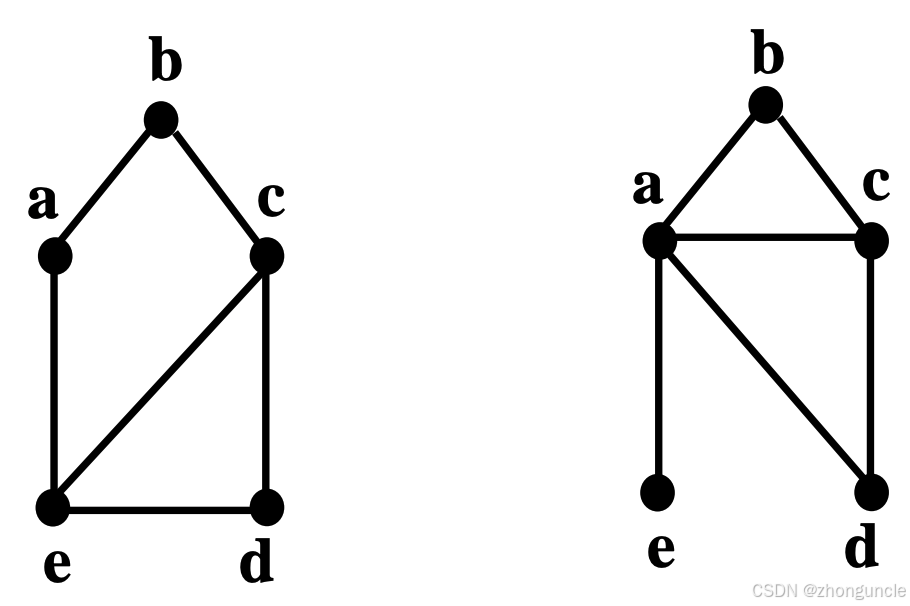
Then take a look at the following graph. You can find that the properties of the graph have changed, because although the number of edges and points remains unchanged, the degree has changed. For example, the degree of e in the left graph is 3, and the degree of e in the right graph is 1, which is not isomorphic.

Complement graph

The mathematical definition of a complement graph is: for a given graph G=(V,E), its complement graph G'=(V,E') is a graph with the same vertex set V, where E' is the set of all possible edges in V that do not appear in E. In other words, the edges in G' are the edges that do not exist in G.

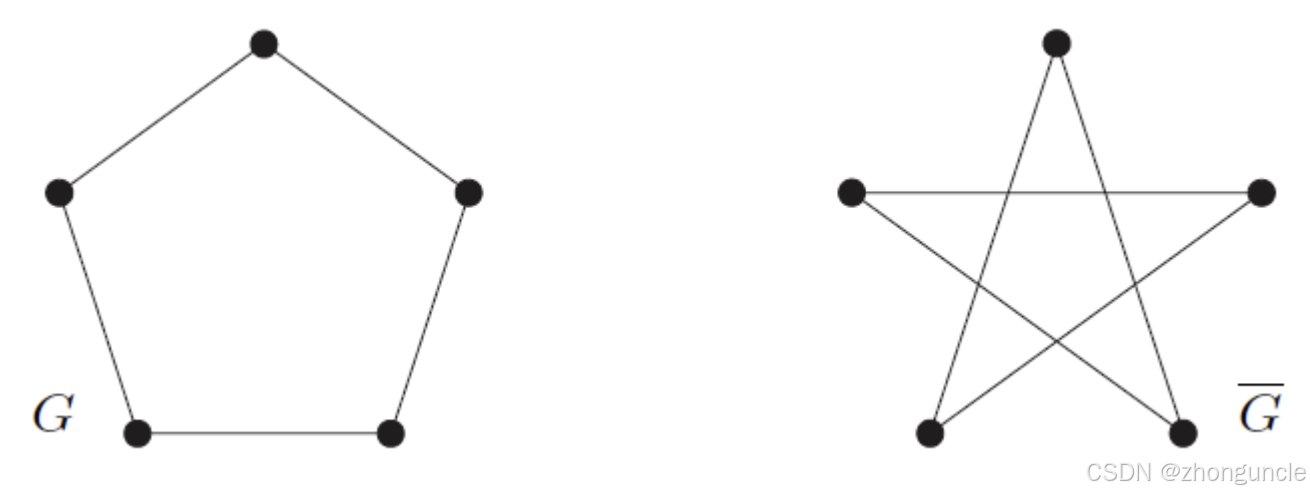
What does it mean? It means that two simple graphs, when put together, are a complete graph, such as the graph mentioned above:

They are a complete graph when put together. Such two graphs are complementary graphs.

Self-complementary graphs

Self-complementary graphs are two graphs that are not only complementary, but also isomorphic.

Still using this example, these two graphs are not only isomorphic, but also complementary, so they are self-complementary graphs.

Sometimes the question will only give one graph and ask whether it is a self-complementary graph. The solution to this problem is to complete the picture first, and then see if the drawn part is isomorphic to the original part.

I hope this can help those in need~