SMA (2/3) Finite automaton string matching algorithm

The finite automaton string matching algorithm requires some number theory knowledge and isn’t particularly engaging.

This article won’t delve into its mathematical properties—explaining them requires readers to have a basic grasp of discrete mathematics; otherwise, we’d first need to clarify several concepts. So if you’re unfamiliar with automata, state machines, sets, relations, or other related concepts and don’t want to learn them, you can just focus on understanding the code below. I’ll provide some conceptual explanations though, since this is also a personal record.

If you do want to understand the underlying mathematics, start by learning discrete mathematics—with an emphasis on number theory. Once you have that foundation, check out Introduction to Algorithms and the University of Chicago’s String Matching with Finite Automata. The latter has better examples, and this article draws some inspiration from it.

What Does the Automaton Do?

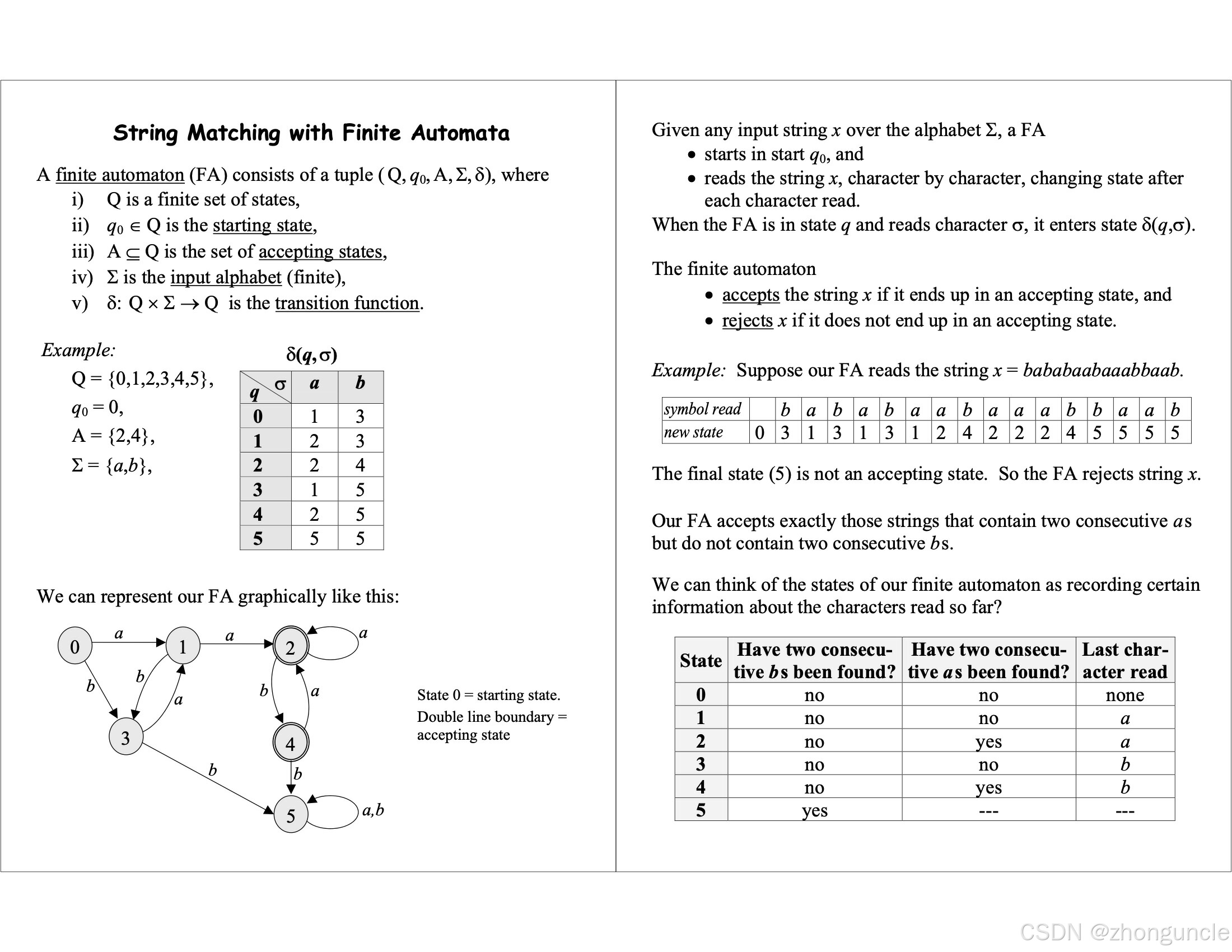
An automaton is a mathematical model consisting of a set of states. Different inputs trigger transitions between these states. Generally, such “machines” are used to implement formal languages or computational models (like the famous Turing machine), but they can also be simulated with programming languages. Finite automata are typically implemented using a state transition table—similar to how graphs are often represented with matrices.

The image below shows a state transition table from Introduction to Algorithms. How is this table constructed, and how do we read it?

This table illustrates how the finite automaton’s state changes based on input:

• The three “input” columns represent possible inputs: a, b, and c. (Inputting d won’t match, so the table’s width often equals the size of the ASCII character set.)
• The row labeled P shows the pattern string we’re matching against.
• Each row represents a state. The first row is the initial state (state 0).
• Each cell indicates the next state to transition to given the current state and input.

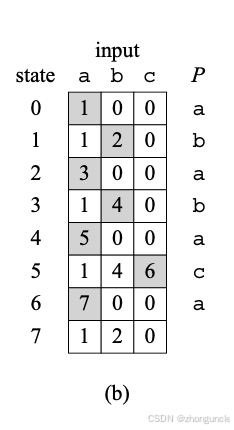
If you’re confused about how to read the table, follow these steps (I arranged them to be visible simultaneously so you don’t have to scroll):

1. Start with the first row (state 0): If the input character (from the string being checked) matches the corresponding character in P, transition to the next state (state 1). For any other input, stay in state 0.
2. Suppose you input a and move to state 1:
   • If the next input is also a, stay in state 1 (equivalent to restarting from state 0 with another a).
   • If the input is b, transition to state 2.
   • If the input is c, return to state 0 (since we need to restart the pattern match from the beginning).
3. Repeat this process until a full match is achieved. When you reach state 7 (the final state), the next input will transition you to state 0, 1, or 2. (To test your understanding, think about why inputting b in the final state returns to state 2.)

Algorithm Logic

From the process above, if there’s any input sequence that leads to state 7, the input string contains the pattern we’re matching. The algorithm logic is roughly as follows:

1. Generate a state transition table (this only depends on the pattern string).
2. “Traverse” the input string using this table. If you reach the final state, the pattern exists in the input.

Generating the State Transition Table

Generating the state transition table is deceptively simple:

• The simple part: For positions where the input character (row) matches the pattern character (column), set the cell value to the next state number (current row + 1).
• The tricky part: What state do we return to if there’s a mismatch? As we saw earlier, returning directly to the initial state (0) can cause errors in some cases. The solution involves backtracking from the current state—but how far back should we go?

First, find the closest previous state where the pattern character matches the current input. Repetition means we might only need to backtrack to the state right after this match. Remember state 1 earlier? Inputting a kept us in state 1 instead of returning to 0.

Next, check incrementally from the start to see if any substring of the pattern matches the substring ending at the current state. If a match is found, we don’t need to restart from the beginning.

For example, in the full code below, you’ll find this snippet handling the backtracking logic:

for (int i = 1; i < state; i++) {
    if (partern[state-i] == in) {
        int j=0;
        for (j = 0; j < state-i; j++) {
            if (partern[j] != partern[i+j]) {
                break;
            }
        }

        if (j == state-i) {
            FA[state][in] = state-(i-1);
            break;
        }
    }
}

What is the line partern[j] != partern[i+j] doing here? Whether the outer loop increments (i++) or decrements (nextState--), this part can be confusing at first.

Some blogs and textbooks use nextState-- instead of i++ and state-i. I prefer the latter—and you’ll understand why after the explanation below.

This code is looking for repeated substrings in the pattern that match the start of the pattern.

Take the pattern ABABAC as an example. If we input B at the C position (a mismatch), we first find the previous B in the pattern:

Pattern:      A B A B A C (input B)
Step 1:                |         (Find the previous B that matches the input)
Step 2:                |__2__|   (The distance between the two Bs is 2—meaning if the substring starting at the beginning matches the substring containing this B, the start substring is shifted right by 2)
Step 3:        |   |             (Start comparing from the shifted position; first character matches)
Step 4:          |   |           (Increment both indices; second character matches)
Step 5:            |   |         (Increment both indices; third character matches)
Step 6:                          (We already confirmed the Bs match when entering the loop, so no need to compare this position)
Step 7:        |_____|           (The substrings match—so we backtrack 2 states)
                |_____|

In other words:

1. Assume there’s a repeated substring that matches the start of the pattern. Calculate how far this substring is shifted from the start.
2. Verify this assumption by comparing the two substrings. If they match, we can backtrack to the state right after the repeated substring. (This is why the code stores state-(i-1) in the transition table instead of state-i.)

That’s the logic behind the code snippet above.

Traversing the State Transition Table

This part is straightforward: feed the input string into the table one character at a time. Here’s how it’s implemented:

for (int i = 0, state = 0; i < lenstr; i++) {
    state = FA[state][str[i]];
    // If we reach the final state, the pattern is found
    if (state == lenpart) {
        printf ("Match starts at index %d\n", i-lenpart+1);
    }
}

Full Code

I referenced some existing implementations when writing this code—initially, I couldn’t figure out how the algorithm worked after reading Introduction to Algorithms. Many sources use a decrementing loop (for with nextState--) to handle backtracking, but it took me a while to understand. I prefer the incrementing approach (i++ and state-i). When I modified it, I forgot to adjust one part and spent an hour debugging—total rookie mistake.

Here’s the complete code:

#include<stdio.h>

// Length equals the size of the ASCII character set
#define NumInput 256

void automataMatch(char str[], char partern[], int lenstr, int lenpart) {
    // Initialize all state transition table values to 0
    int FA[lenpart+1][NumInput];
    for (int i=0; i<(lenpart+1); i++) {
        for (int j=0; j<NumInput; j++) {
            FA[i][j] = 0;
        }
    }
 
    // Build the state transition table
    for (int state = 0; state <= lenpart; state++) {
        for (int in = 0; in < NumInput; in++) {
            // If current state's pattern character matches the input
            if (state < lenpart && in == partern[state]) {
                FA[state][in] = state + 1;
            } else {
                // Handle mismatch: determine the state to backtrack to
                /*  For example, with the pattern "ababaca" from the table:
                    If we input 'b' at the 'c' position (state=6), we backtrack to find a previous 'b'.
                    We find it at position 4 (preState = state-2 = 4).
                    We then check if the substring starting at state 2 matches the start of the pattern.
                    If all characters match, we return to that state.
                 */
                for (int i = 1; i < state; i++) {
                    if (partern[state-i] == in) {
                        int j=0;
                        for (j = 0; j < state-i; j++) {
                            if (partern[j] != partern[i+j]) {
                                break;
                            }
                        }

                        if (j == state-i) {
                            FA[state][in] = state-(i-1);
                            break;
                        }
                    }
                }
            }
        }
    }
    
    // Start matching the input string
    for (int i = 0, state = 0; i < lenstr; i++) {
        state = FA[state][str[i]];
        // If we reach the final state, the pattern is found
        if (state == lenpart) {
            printf ("Match starts at index %d\n", i-lenpart+1);
        }
    }
    
}

int main(void)
{
    char str[]="ABABAC";
    char partern[]="ABA";

    int lenstr=sizeof(str)/sizeof(char)-1;
    int lenpart=sizeof(partern)/sizeof(char)-1;
    
    automataMatch(str, partern, lenstr, lenpart);
    
    return 0;
}

The string here is different from the earlier example to demonstrate multiple matches. The output is:

Match starts at index 0
Match starts at index 2

Next article: SMA (3/3) KMP (Knuth–Morris–Pratt) string matching algorithm - ZhongUncle GitHub Pages

I hope these will help someone in need~